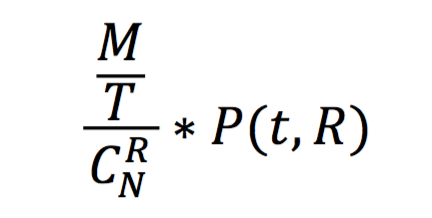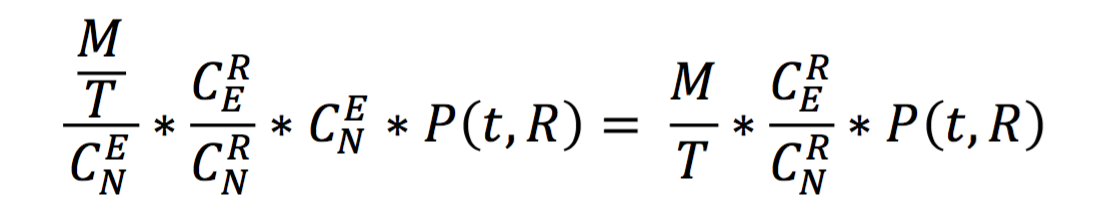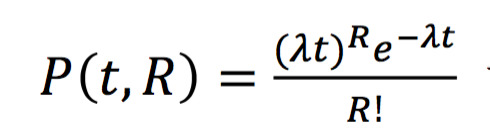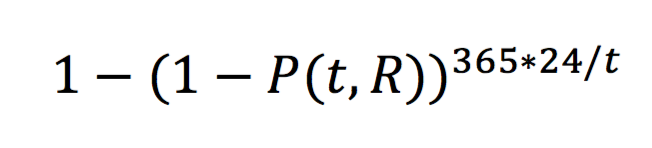对三副本与ErasureCode两种方式下，数据丢失概率的估算，组合数学和概率论知识早就还给老师了，贴到博客给大家看看计算方法是否正确。

1. 对于R个副本的情况，设磁盘年故障概率为P，磁盘数为N，则整个机群有C(N, R) = N!/(R!*(N-R)!)种R副本的组合方式。机群数据总量为M，分片大小为T，那么有R个磁盘同时损坏造成数据丢失的概率是：

2. 对于由E个块组成的EC组，假设最多允许R-1个块丢失，整个机群有C(N, E)种EC组的组合方式，因此有R个磁盘同时损坏造成数据丢失的概率是：

其中P(t, R)表示在t时间内连续损坏R块磁盘的概率，这个概率符合泊松分布即：

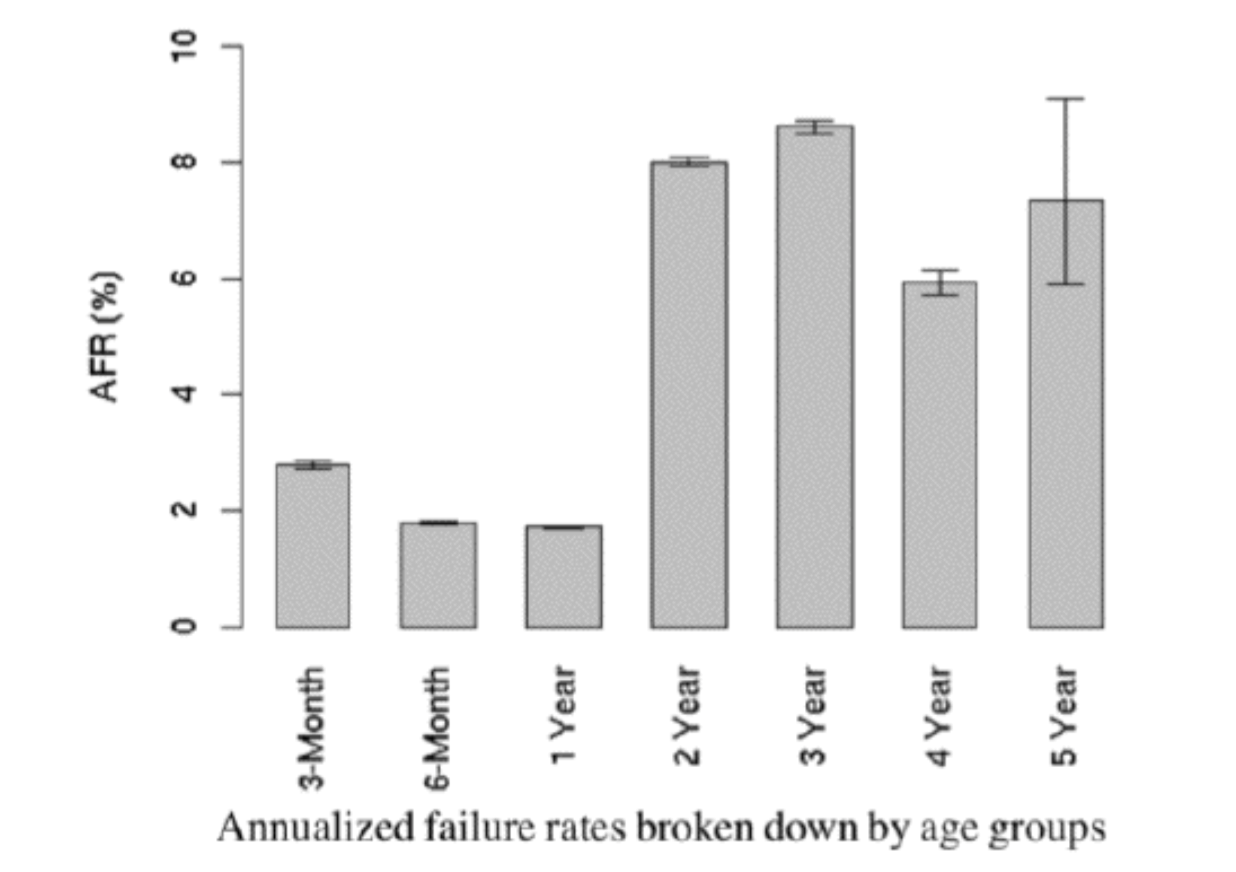
设为t的单位时间(设为1小时)内发生磁盘损坏的平均次数，根据google的统计，磁盘的年失败率(AFR: Fnnualized Failure Rate)如下图所示，我们取一个平均值4来进行计算。那么就是0.0004566。

年故障率：

假设单盘容量为6T，使用率为70%，数据分片大小为1GB，在一个1000块磁盘的集群中，不同恢复时间的年故障率对比为：

恢复用时	3副本年故障率	EC(8+4)年故障率
1	1.2 * 10E-9	4.0 * 10E-19
4	1.9 * 10E-8	1.0 * 10E-16
12	1.7 * 10E-7	8.2 * 10E-15
24	6.8 * 10E-7	1.3 * 10E-13

3副本的恢复代价较小，因此我们可以按照机群使用1小时恢复单盘数据，EC恢复代价比较大，因此我们按照机群使用24小时恢复单盘数据，这两种情况下的持久性分布达到11个9和13个9。

附Python计算代码：

#!/usr/bin/python
# -*- coding: utf-8 -*-
import decimal
import math

lamda=decimal.Decimal(str(4.0/24/365))
e=decimal.Decimal(str(math.e))
perC=6.0*0.7*1024 #单盘容量(T)*使用率

#级数
def factorial(n):
  S = decimal.Decimal("1")
  for i in range(1, n+1):
    N = decimal.Decimal(str(i))
    S = S*N
  return S

#组合运算
def C(n, m):
  return factorial(n) / (factorial(m)*factorial(n-m))

#泊松分布
def poisson(t, R):
  return ((lamda * t) ** R) * (e**(-lamda*t)) / factorial(R)

#t时间内损坏R块磁盘的概率
def probability(t, R):
  return poisson(t, R)

#多副本年失效概率, T=分片大小(G), N=磁盘个数, t=单盘故障的复制时间, R=副本数
def probability_3R(T, N, t, R):
  M = decimal.Decimal(str(N * perC / R))
  pt = M / T / C(N,R) * probability(t, R)
  return (1 - (1-pt)**(decimal.Decimal(str(365.0*24/t))))

#EC年失效概率, T=分片大小(G), N=磁盘个数, t=单盘故障的复制时间, R=损坏超过R块磁盘则可能丢数据, E=EC组大小
def probability_EC(T, N, t, R, E):
  M = decimal.Decimal(str(N * perC / (1.0 * E / (E - R + 1))))
  pt = (M / T) * C(E,R) / C(N,R) * probability(t, R)
  return (1 - (1-pt)**(decimal.Decimal(str(365.0*24/t))))